Με βάση τα νεότερα στοιχεία για τον SAR-CoV-2 υπολογίζεται πως κάθε άτομο που νοσεί είναι υπεύθυνο για τη μόλυνση 2-3 ακόμα ατόμων. Αυτή η μόλυνση θα συμβεί, πιο πιθανά, στο διάστημα 4-6 ημερών (έστω 5), όπου θα εμφανίζει έντονα συμπτώματα και το αρχικό άτομο θα είναι, συνεπώς, πιο μεταδοτικό. Άρα, ξεκινώντας τη μέρα μηδέν με ένα άτομο που νοσεί, σε 5 μέρες θα νοσούν 3 άτομα (το αρχικό και 2 ακόμα που θα έχει μολύνει). Μέσα στις επόμενες 5 μέρες, κάθε ένα από αυτά τα καινούργια άτομα θα μολύνει 2 ακόμα, οπότε θα νοσούν συνολικά 6 άτομα (αν υποθέσουμε ότι το άτομο 0 έχει πλέον αναρρώσει).
Ακολουθώντας τους ίδιους κανόνες μετά από 5 ακόμα μέρες θα έχουμε 12 άτομα που νοσούν. Μετά από 10 μέρες, 24 άτομα. Παρατηρούμε λοιπόν, ότι ο αριθμός των νοσούντων ακολουθεί εκθετική καμπύλη αύξησης με χρόνο διπλασιασμού τις 5 μέρες και R0=2 Στο τέλος ενός μήνα τα κρούσματα θα έχουν φτάσει στα 96.
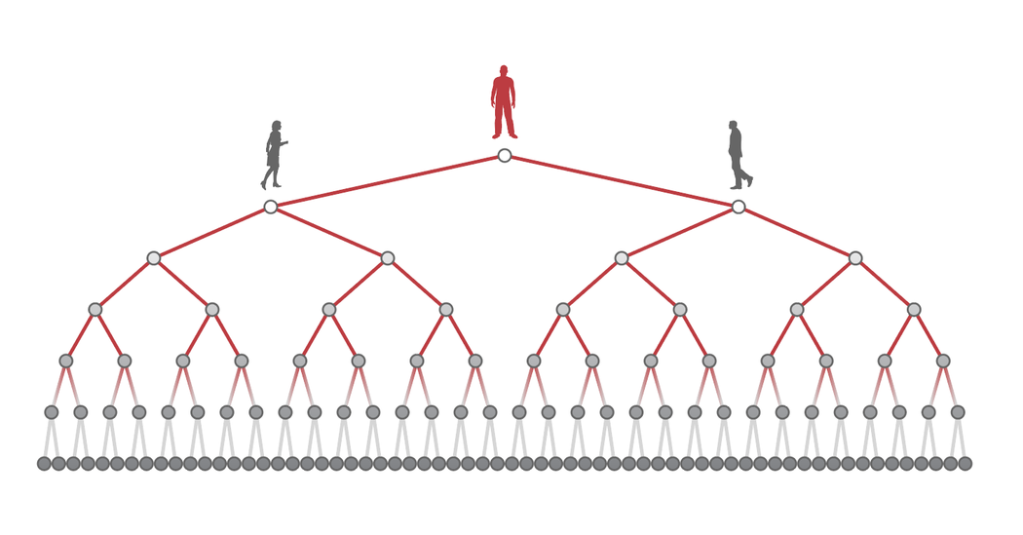
Ο αριθμός των κρουσμάτων στο τέλος του δεύτερου μήνα ανέρχεται σε 6.144. Βλέπουμε λοιπόν, ότι μικρές και φαινομενικά ασήμαντες αλλαγές μέσα στον πρώτο μήνα, οδηγούν σε ραγδαία αύξηση μέσα σε σύντομο χρονικό διάστημα. Είναι δύσκολο να προβλέψεις μια τέτοια εξέλιξη κοιτώντας την αρχική πορεία της επιδημίας. Η ίδια η φύση της εκθετικής καμπύλης την καθιστά δύσκολη στην κατανόηση. Αυτά τα νούμερα όμως δεν θα έπρεπε να είναι λόγος πανικού. Αφού μπορούμε να προβλέψουμε την πορεία της καμπύλης, μπορούμε να βρούμε και αποτελεσματικούς τρόπους να αλλάξουμε αυτή την πορεία. Να μειώσουμε το R, να «επιπεδώσουμε» την καμπύλη.
Παραθέτουμε εδώ, ένα παράδειγμα της μορφής που θα έπαιρνε η καμπύλη αν η επιδημία εξελισσόταν χωρίς αναχαιτιστικούς παράγοντες (μωβ καμπύλη).
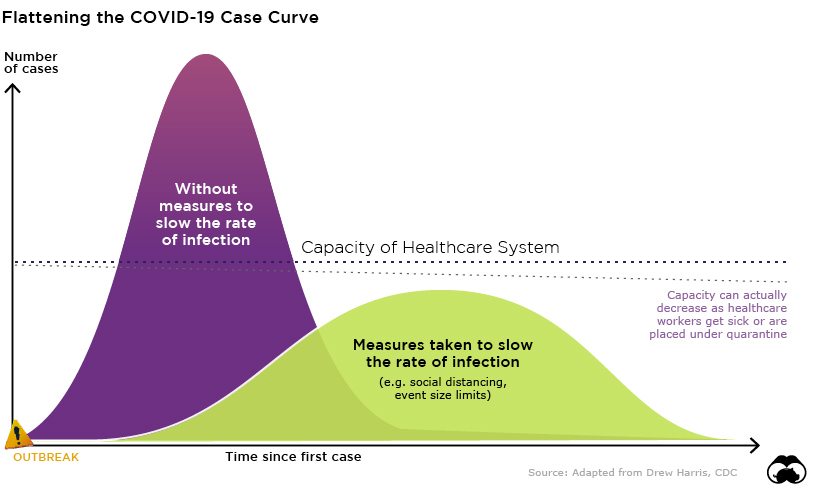
Από αυτή την εικόνα, απορρέουν όλα τα δημοσιεύματα που θέλουν το μέσο για την επίλυση της κατάστασης ανάγκης να είναι το «Flatten the curve – Raise the line». Παρατηρούμε ότι η καμπύλη δεν ανεβαίνει επ’ αόριστον. Σε κάποιο σημείο γίνεται σταθερή και έπειτα ακολουθεί καθοδική πορεία. Αυτό συμβαίνει επειδή σε ένα πληθυσμό, μόλις μολυνθεί ένα αρκετά μεγάλο ποσοστό, και δεδομένου ότι άτομα που αναρρώνουν δεν μπορούν να επαναπροσβληθούν, ο ιός δεν βρίσκει εύκολα αλλά άτομα να μολύνει. Καθίσταται έτσι αδύνατο κάθε άτομο που νοσεί να μολύνει 2 άτομα. Συνεπώς, το R μειώνεται, και η καμπύλη πέφτει (για περισσότερες πληροφορίες πάνω στα R και R0 μπορείτε να διαβάσετε το προηγούμενο άρθρο μας https://covidgr.net/2020/05/03/τι-ακριβώς-είναι-το-r0-και-γιατί-θέλουμε/) . Αυτή η πτώση αντιπροσωπεύει και την δράση της ανοσίας αγέλης, όπου η ανοσία που έχει δημιουργηθεί στην κοινότητα από τα άτομα που έχουν ήδη νοσήσει, προστατεύει την υπόλοιπη κοινότητα.
Στο ίδιο γράφημα παρατηρούμε ότι υπάρχει και μια διακεκομμένη γραμμή. Η γραμμή αυτή αντιπροσωπεύει τον αριθμό των κρουσμάτων που μπορεί να διαχειριστεί το σύστημα υγείας μας. Είναι εμφανές, ότι η ραγδαία αύξηση των κρουσμάτων σε μικρό χρονικό διάστημα, οδηγεί την καμπύλη πολύ πιο ψηλά από την χωρητικότητα του συστήματος υγείας. Μια τέτοια εξέλιξη θα οδηγούσε και σε αύξηση της θνητότητας. Για την αντιμετώπιση των βαριά ασθενών, χρειάζεται εισαγωγή σε Μονάδα Εντατικής Θεραπείας για υποστήριξη του αναπνευστικού συστήματος το οποίο ανεπαρκεί. Χωρίς αυτή την παρέμβαση, οι πιθανότητες επιβίωσής τους μειώνονται δραματικά. Επειδή στις περισσότερες χώρες του κόσμου η χωρητικότητα σε κλίνες ΜΕΘ είναι περιορισμένη, πρωταρχικός στόχος είναι να γίνει αρκετά επίπεδη η καμπύλη ώστε να μην καλυφθούν όλες οι κλίνες ΜΕΘ. Αυτό θα εξασφάλιζε μικρότερη συμφόρηση του συστήματος υγείας, υποφερτό φόρτο εργασίας για τους υγειονομικούς υπαλλήλους, και αποφυγή των αποκαρδιωτικών καταστάσεων που θέλουν τους γιατρούς να επιλέγουν ποιος ασθενής αξίζει να διασωληνωθεί.
Πως, λοιπόν, θα γίνει επίπεδη η καμπύλη?
Μειώνοντας το R. Μπορούμε να θεωρήσουμε το R ως την κλίση της καμπύλης. Όσο μεγαλύτερο το R, τόσο πιο απότομα ανεβαίνει η καμπύλη και περισσότερα άτομα είναι άρρωστα στο ίδιο, μικρό χρονικό διάστημα. Αν αυτό συνέβαινε, θα κατέρρεε το σύστημα υγείας μας. Αν το R μειωνόταν, ακόμα και αν, σε βάθος χρόνου, μολυνόταν από τον ιό ο ίδιος αριθμός ατόμων, αυτό θα γινόταν σε μεγαλύτερο χρονικό διάστημα, οπότε το σύστημα υγείας θα μπορούσε να διαχειριστεί τον αριθμό των ασθενών ανά πάσα στιγμή (βλέπε πράσινο διάγραμμα). Έτσι, όλοι οι βαριά ασθενείς θα λάμβαναν την ιατρική φροντίδα που χρειάζονταν και η συνολική θνητότητα θα ήταν πολύ χαμηλότερη σε σύγκριση με το προηγούμενο σενάριο. Φυσικά, η ελπίδα είναι να μην χρειαστεί να νοσήσει τόσο μεγάλη μερίδα του πληθυσμού ώστε να λειτουργήσει η ανοσία αγέλης, αλλά να δημιουργηθεί ένα εμβόλιο που θα δημιουργήσει ανοσία στην κοινότητα χωρίς να χρειαστεί να τεθούν σε κίνδυνο ανθρώπινες ζωές με πραγματική μόλυνση με τον ιό.
Η στρατηγική μείωσης του R, λοιπόν, αποσκοπεί στο να κερδίσουμε χρόνο. Χρόνο για να βρούμε αποτελεσματική θεραπεία για να βοηθήσουμε όσους ασθενούν από τον ιό. Χρόνο για να δημιουργήσουμε εμβόλιο. Χρόνο για να «θωρακίσουμε» το σύστημα υγείας μας ώστε η περίθαλψη να είναι επαρκής, ακόμα και σε καταστάσεις έξαρσης μιας επιδημίας.

